Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án - Tuyensinh247 (đề 1)

CẤU TRÚC BÀI THI

---------------------------------------------------

NỘI DUNG BÀI THI

BIÊN SOẠN: BAN CHUYÊN MÔN TUYENSINH247.COM

PHẦN I – TƯ DUY TOÁN HỌC

Câu 1: Cho số phức \(z = {\rm{\;}} - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\). Mô đun số phức \(1 + z + {z^2}\) bằng:……..

Câu 2: Tính giá trị biểu thức \(T = {\left| {{z_1} - {z_2}} \right|^2}\), biết \({z_1},{z_2}\) là các số phức thỏa mãn đồng thời \(\left| z \right| = 5\) và \(\left| {z - \left( {7 + 7i} \right)} \right| = 5\).

A. 10

B. 2

C. 3

D. 4

Câu 3: Trong tập số phức, cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_n} = 1\) và công bội là \(q = 1 + i\). Dãy số \(\left( {{v_n}} \right)\) là dãy số thỏa mãn \({v_n} = \left| {{u_n}} \right|\forall n \ge 1\). Mỗi phát biểu sau đúng hay sai?

Câu 4: Cho hàm số \(f\) liên tục trên đoạn [a ; b]. Giả sử hàm số \(u = u(x)\) có đạo hàm liên tục trên đoạn [a ; b] và \(\alpha  \le u(x) \le \beta \). Giả sử có thể viết \(f(x) = g(u(x)){u^\prime }(x),x \in [a;b]\), với \(g\) liên tục trên đoạn \([\alpha ;\beta ]\). Khi đó, mệnh đề nào sau đây đúng?

A. \(\int_a^b f (x)dx = \int_a^b u (x)du\)

B. \(\int_a^b f (x)dx = \int_{u(b)}^{u(a)} g (u)du\)

C. \(\int_a^b g (x)dx = \int_{u(a)}^{u(b)} f (u)du\)

D. \(\int_a^b f (x)dx = \int_{u(a)}^{u(b)} g (u)du\)

Câu 5: Cho \(\lim {u_n} = L\). Chọn mệnh đề đúng:

A. \(\lim \sqrt[3]{{{u_n}}} = L\)

B. \(\lim \sqrt {{u_n}} {\rm{\;}} = L\)

C. \(\lim \sqrt {{u_n}} {\rm{\;}} = \sqrt L \)         

D. \(\lim \sqrt[3]{{{u_n}}} = \sqrt[3]{L}\)

Câu 6: Giá trị trung bình của hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) được tính theo công thức \(m\left( f \right) = \dfrac{1}{{b - a}}\int\limits_a^b {f\left( x \right)} d{\rm{x}}\). Xét \(f\left( x \right) = 3{x^2} - 2x\) và giá trị trung bình của hàm số trên [-1;1], có bao nhiêu giá trị của c thuộc đoạn [-1;1] thỏa mãn: \(m\left( f \right) = f\left( c \right)\).

A. \(\dfrac{1}{3}\)

B. \(1\)

C. \(2\)

D. \(\dfrac{2}{3}\)

Câu 7: Số dân của một thị trấn sau \(t\) năm kể từ năm 1990 được ước tính bởi công thức

\(f(t) = \dfrac{{14t + 10}}{{t + 5}}\)

( \(f(t)\) được tính bằng nghìn người).

Câu 8: Diện tích phần hình phẳng giới hạn bởi đồ thị hai hàm số \({y^2} = ax\left( {a > 0} \right)\) và \(x = a\) bằng \(k.{a^2}\). Tính \(k\).

A. \(\dfrac{8}{3}\)

B. \(\dfrac{2}{3}\)

C. \(\dfrac{4}{3}\)

D. \(\dfrac{1}{3}\)

Câu 9: Trong bốn hàm số \(y = {x^4} - 5{x^2},y =  - {x^3} + 2{x^2} + 1,\) \(y = {x^2} - 3x - 1,y = \dfrac{{1 - x}}{{2x + 1}}\) số lượng các hàm số đồng biến trên khoảng \(\left( {2;3} \right)\) là:

A. 1

B. 3

C. 2

D. 4

Câu 10: Một khối chóp tam giác có các cạnh đáy bằng 15;8;17. Một cạnh bên có độ dài bằng 4 và tạo với mặt đáy góc \({45^0}\). Thể tích của khối chóp đó bằng

A. \(60\sqrt 2 \)

B. \(30\sqrt 2 \)

C. \(40\sqrt 2 \)

D. \(80\sqrt 2 \)

Câu 11: Trong không gian Oxyz, cho điểm \(M(4;6;4)\) và hai đường thẳng \({d_1}:\dfrac{{x - 1}}{2} = \dfrac{{y + 3}}{4} = \dfrac{z}{3}\), \({d_2}:\dfrac{x}{1} = \dfrac{{y - 2}}{1} = \dfrac{{z + 4}}{3}\). Đường thẳng đi qua \(M\) đồng thời cắt cả 2 đường thẳng \({d_1}\) và \({d_2}\) tại \(A\) và \(B\), độ dài đoạn thẳng AB bằng

A. \(\sqrt {43} \).

B. \(2\sqrt {43} \).

C. \(2\sqrt {13} \).

D. \(\sqrt {13} \).

Câu 12. Trong không gian Oxyz, cho điểm \(M( - 1;0;2)\) và mặt phẳng \((P):x - 2y + 4z + 1 = 0\). Đường thẳng đi qua \(M\) và vuông góc với \((P)\) có phương trình là:

A. \(\dfrac{{x + 1}}{1} = \dfrac{y}{{ - 2}} = \dfrac{{z - 2}}{1}\).

B. \(\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z + 2}}{1}\).

C. \(\dfrac{{x + 1}}{1} = \dfrac{y}{{ - 2}} = \dfrac{{z + 2}}{4}\).

D. \(\dfrac{{x + 1}}{{ - 1}} = \dfrac{y}{2} = \dfrac{{z - 2}}{{ - 4}}\).

Câu 13: Xếp loại học lực các học sinh khối 11 của một trường THPT được cho bởi biểu đồ dưới đây:

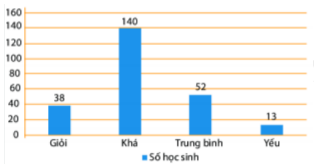
Chọn ngẫu nhiên một học sinh để phát biểu trong lễ tổng kết. Xác suất để chọn được học sinh khá lên phát biểu là

A. \(\dfrac{{38}}{{243}}\).

B. \(\dfrac{{140}}{{243}}\).

C. \(\dfrac{{52}}{{243}}\).

D. \(\dfrac{{13}}{{243}}\).

Câu 14: Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9, có thể lập được bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau sao cho tổng ba chữ số hàng trăm, hàng chục và hàng đơn vị bằng 6?

Câu 15: Cho hình vuông \(ABCD\) có các cạnh bằng \(a\) và có diện tích bằng \({S_1}\). Nối bốn trung điểm \({A_1},\,{B_1},\,{C_1},\,{D_1}\) theo thứ tự của bốn cạnh \(AB,\,BC,\,CD,\,DA\) ta được hình vuông thứ hai có diện tích \({S_2}\).

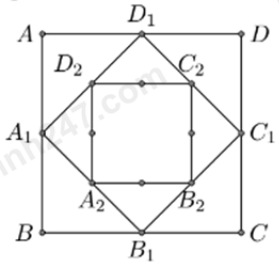
Tiếp tục quá trình trên ta được hình vuông thứ ba là \({A_2}{B_2}{C_2}{D_2}\) có diện tích \({S_3}\) … và cứ tiếp tục như thế ta được các hình vuông lần lượt có diện tích \({S_4},\,{S_5},\,...,{S_{50}}\) (tham khảo hình vẽ). Tổng \(S = {S_1} + {S_2} + ... + {S_{50}}\) bằng

A..\(\dfrac{{{a^2}\left( {{2^{50}} - 1} \right)}}{{{2^{49}}}}\)

B. \(\dfrac{{{a^2}\left( {{2^{50}} - 1} \right)}}{{{2^{50}}}}\)

C. \(\dfrac{{{a^2}\left( {{2^{49}} - 1} \right)}}{{{2^{48}}}}\)

D. \(\dfrac{{{a^2}}}{{{2^{50}}}}\).

Câu 16: Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

a) Hàm số \(y = \sin x + 5\) tuần hoàn với chu kì …………

b) Hàm số \(y = \cot x\) không xác định với mọi \(x\) có dạng ………… (\(k \in \mathbb{Z}\)).

Câu 17: Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Một hình trụ có thiết diện qua trục là hình vuông và có diện tích xung quanh bằng \(36\pi \). a) Bán kính hình trụ là ………

b) Thể tích lăng trụ lục giác đều nội tiếp hình trụ là …………

Câu 18: Xét các số phức \(z\) thỏa mãn \(|z| = \sqrt 2 \) và số phức \(w = \dfrac{{2 + iz}}{{1 + z}}\).

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

Câu 19: Trong không gian \(Oxyz\), cho đường thẳng \(d:\dfrac{{x + 1}}{2} = \dfrac{y}{1} = \dfrac{{z - 2}}{{ - 1}}\) và hai điểm \(A\left( { - 1;3;1} \right)\); \(B\left( {0;2; - 1} \right)\). Gọi \(C\left( {m;n;p} \right)\) là điểm thuộc đường thẳng \(d\) sao cho diện tích tam giác \(ABC\) bằng \(2\sqrt 2 \). Giá trị của tích \(m.n.p\) bằng ……….

Câu 20: Gọi \({m_0}\) là giá trị thực của tham số \(m\) để giá trị lớn nhất của hàm số \(y = \dfrac{{ - x + {m^2} + 1}}{{x + 2}}\) trên đoạn \([2;\,5]\) bằng \(1\). Khi đó, giá trị của \({m_0}\) có thể thuộc những khoảng nào trong các khoảng sau?

A. \((0;\,2)\).

B. \((2;\,3)\).

C. \(( - 4; - \,2)\).

D. \(( - 1;\,1)\).

Câu 21: Một vật chuyển động có phương trình \(s(t) = {t^4} - 3{t^3} - 3{t^2} + 2t + 1\,(m)\), với \(t(s)\)là thời gian chuyển động. Gia tốc của vật tại thời điểm \(t = 3s\) là

A. \(48(m/s)\).

B. \(28(m/{s^2})\).

C. \(48(m/{s^2})\).

D. \(54(m/{s^2})\).

Câu 22: Cô Hà hàng tháng gửi vào ngân hàng 2 triệu đồng với lãi suất 0,6%/tháng. Sau 1 năm, cô Hà rút cả vốn lẫn lãi về mua vàng thì số chỉ vàng cô Hà mua được ít nhất là bao nhiêu? (Biết giá vàng tại thời điểm mua là 5,36 triệu đồng/chỉ).

Câu 23: Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(2\). Khoảng cách giữa hai đường thẳng \(AC\) và \(B'D'\) là 

A. \(\sqrt 2 \).

B. \(4\).

C. \(2\).

D. \(2\sqrt 2 \).

Câu 24: Nếu m là số nguyên dương, a và b chia cho m có cùng số dư thì ta nói a đồng dư với b theo mô đun m, kí hiệu \(a \equiv b\left( {\bmod m} \right)\). Khẳng định nào sau đây đúng?

A. \({3^5} \equiv 1\left( {\bmod 4} \right)\)

B. \({3^5} \equiv 2\left( {\bmod 4} \right)\)

C. \({3^5} \equiv 0\left( {\bmod 4} \right)\)

D. \({3^5} \equiv 3\left( {\bmod 4} \right)\)

Câu 25: Cho hàm số f(x) có đạo hàm \(f'(x)\) = \(\dfrac{{(x - 3){{(x + 1)}^2}}}{{\sqrt {x - 1} }}\).Khẳng định nào sau đây là đúng?

A. Hàm số nghịch biến trên khoảng \(( - \infty ; - 1)\)

B. Hàm số đồng biến trên các khoảng \(( - \infty ;1)\) và \((3; + \infty )\)

C. Hàm số đồng biến trên các khoảng (-1; 1) và \((3; + \infty )\)

D. Hàm số đồng biến trên khoảng \((3; + \infty )\)

Câu 26: 

Cho hình nón \(\left( N \right)\) có góc ở đỉnh bằng 120 độ. Mặt phẳng qua trục của \(\left( N \right)\) cắt \(\left( N \right)\) theo một thiết diện là tam giác có đường kính đường tròn ngoại tiếp bằng \(8\). Tính thể tích khối nón \(\left( N \right)\)

A. \(8\pi \).

B. \(4\sqrt 3 \pi \).

C. \(16\pi \)

D. \(6\pi \)

Câu 27: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Một mặt phẳng thay đổi, vuông góc với cắt SO, SA, SB, SC, SD lần lượt tại I, M,N,P,Q. Một hình trụ có một đáy nội tiếp tứ giác MNPQ và một đáy nằm trên hình vuông ABCD. Khi thể tích khối trụ lớn nhất thì độ dài SI bằng

A. \(SI = \dfrac{{3a\sqrt 2 }}{2}\).

B. \(SI = \dfrac{{a\sqrt 2 }}{2}\).

C. \(SI = \dfrac{{a\sqrt 2 }}{3}\).

D. \(SI = \dfrac{a}{3}\).

Câu 28: Cho mặt cầu \((S):{x^2} + {y^2} + {z^2} - 2x + 4y + 2z - 3 = 0\) và mặt phẳng \((P):x + y - 2z + 4 = 0\). Phương trình đường thẳng \(d\) tiếp xúc với mặt cầu \((S)\) tại \(A(3; - 1;1)\) và song song với mặt phẳng \((P)\) là:

A. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 4t}\\{y =  - 1 + 6t}\\{z = 1 + t}\end{array}} \right.\)

B. \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 4t}\\{y =  - 2 - 6t}\\{z =  - 1 - t}\end{array}} \right.\)

C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 4t}\\{y =  - 1 - 6t}\\{z = 1 - t}\end{array}} \right.\)

D. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 2t}\\{y =  - 1 + t}\\{z = 1 + 2t}\end{array}} \right.\)

Câu 29: Hệ số của \({x^{14}}\) trong khai triển \({\left( {{x^2} - 3x} \right)^{10}}\) là ……..

Câu 30: Từ các chữ số 0; 1; 2; 3; 4; 5 có thể lập thành bao nhiêu số có 4 chữ số đôi một khác nhau và chia hết cho 5?

A. 108

B. 120

C. 200.

D. 240

Câu 31: Cho khối lăng trụ tam giác đều ABC.A'B'C' có \(AB = a\), góc giữa đường thẳng A'B và mặt phẳng \(\left( {BCC'B'} \right)\) bằng 30 độ. Thể tích khối lăng trụ đã cho bằng:

A. \(\dfrac{{\sqrt 3 }}{2}{a^3}\).

B. \(\dfrac{{\sqrt 6 }}{4}{a^3}\).

C. \(\dfrac{3}{4}{a^3}\).

D. \(\dfrac{{\sqrt 6 }}{{12}}{a^3}\).

Câu 32: Tổng sau: \(S = \left[ {\sqrt 1 } \right] + \left[ {\sqrt 2 } \right] + ... + \left[ {\sqrt {24} } \right]\) bằng ……

Câu 33: Có bao nhiêu cặp số thực \((a;b)\) để bất phương trình \((x - 1)(x + 2)(a{x^2} + bx + 2) \ge 0\) nghiệm đúng với mọi \(x \in \mathbb{R}\)?

A. \(3\).

B. \(2\).

C. \(0\).

D. \(1\).

Câu 34: Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng toạ độ Oxy là một parabol có phương trình \(y =  - \dfrac{1}{{10}}{x^2} + x\), trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất (tham khảo hình vẽ). Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O (khoảng cách này được gọi là tầm xa của quỹ đạo).

A. \(6(\;{\rm{m}})\)

B. \(7(\;{\rm{m}})\)

C. \(13(\;{\rm{m}})\)

D. \(10(\;{\rm{m}})\)

Câu 35: Ba tia Ox,Oy,Oz đôi một vuông góc, \(C\) là một điểm cố định trên Oz, đặt \(OC = 1\). A,B thay đổi trên Ox,Oy sao cho \(OA + OB = OC\). Tính giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC.

A. \(\dfrac{{\sqrt 6 }}{4}\)

B. \(\dfrac{{\sqrt 6 }}{3}\)

C. \(\dfrac{{\sqrt 6 }}{2}\) 

D. \(\sqrt 6 \)

Câu 36: Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình  \(m < \dfrac{{{3^x} + {2^x}}}{{{3^x} - {2^x}}}\) nghiệm đúng với mọi \(x \in \left( {0; + \infty } \right)\)

A. 10

B. 1

C. 9

D. 8

Câu 37: Cho hai số thực dương a,b thỏa mãn \(2 + {\log _2}a = 1 + {\log _5}b = {\log _{10}}(a + b)\). Giá trị của biểu thức \(\dfrac{1}{a} + \dfrac{1}{b}\) là?

A. 20

B. 10

C. 12

D. 2

Câu 38: Cho các số dương x,y thoả mãn \({\log _5}\left( {\dfrac{{x + y - 1}}{{2x + 3y}}} \right) + 3x + 2y \le 4\). Giá trị nhỏ nhất của biểu thức \(A = 6x + 2y + \dfrac{4}{x} + \dfrac{9}{y}\) bằng

A. \(\dfrac{{27\sqrt 2 }}{2}\).

B. \(\dfrac{{31\sqrt 6 }}{4}\).

C. \(11\sqrt 3 \).

D. 19

Câu 39: Cho \(x,\,y\) là các số thực lớn hơn 1 thỏa mãn \({x^2} - 6{y^2} = xy\). Khi đó, giá trị của biểu thức \(M = \dfrac{{1 + {{\log }_{12}}x + {{\log }_{12}}y}}{{2{{\log }_{12}}\left( {x + 3y} \right)}}\) thuộc những khoảng nào sau đây?

A. \((0;2)\).

B. \((1;5)\).

C. \(( - 1;1)\).

D. \(( - 1;3)\).

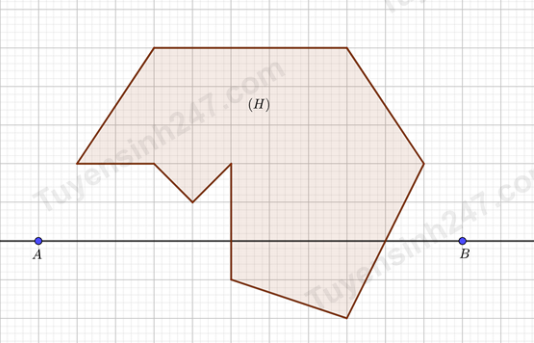
Câu 40: Ở hình vẽ dưới đây, mỗi ô vuông có cạnh \(1\,cm\) và được chia thành 25 ô vuông nhỏ. Miền đa giác thu được khi lấy hình \((H)\) hợp với ảnh đối xứng của nó qua trục \(AB\) có diện tích bằng ………… \(c{m^2}\).

PHẦN II – TƯ DUY ĐỌC HIỂU

Đọc văn bản sau và trả lời các câu hỏi từ 1 đến 7: 

CÔNG NGHỆ AI CỦA HIỆN TẠI VÀ TƯƠNG LAI

[0] Công nghệ AI (Artificial Intelligence) hiện đang là công nghệ được quan tâm phát triển và ứng dụng bậc nhất hiện nay, được ứng dụng trong nhiều lĩnh vực như nhận dạng khuôn mặt, xử lý giọng nói, kỹ thuật ước tính đám đông … đến các hệ thống an ninh, bảo mật, hay hệ thống pháp luật, chính phủ.

Hình 1. Trí tuệ nhân tạo (AI) là lĩnh vực của ngành khoa học máy tính và công nghệ thông tin (Ảnh nguồn INEC)

[1] Theo dòng chảy của cuộc cách mạng 4.0, trí tuệ nhân tạo ngày càng được phổ biến và ứng dụng rộng rãi trong mọi lĩnh vực của cuộc sống, mặc dù được John McCarthy – nhà khoa học máy tính người Mỹ đề cập lần đầu tiên vào những năm 1950 nhưng đến ngày nay thuật ngữ trí tuệ nhân tạo mới thực sự được biết đến rộng rãi và được các “ông lớn” của làng công nghệ chạy đua phát triển.

[2] AI là công nghệ sử dụng đến kỹ thuật số có khả năng thực hiện những nhiệm vụ mà bình thường phải cần tới trí thông minh của con người, được xem là phổ biến nhất. Đặc trưng của công nghệ AI là năng lực “tự học” của máy tính, do đó có thể tự phán đoán, phân tích trước các dữ liệu mới mà không cần sự hỗ trợ của con người, đồng thời có khả năng xử lý dữ liệu với số lượng rất lớn và tốc độ cao. Hiện mỗi ngày trên toàn cầu có khoảng 2,2 tỷ Gb dữ liệu mới (tương đương 165.000 tỷ trang tài liệu) được tạo ra và được các công ty, như Google, Twitter, Facebook, Amazon, Baidu, Weibo, Tencent hay Alibaba thu thập để tạo thành “dữ liệu lớn” (big data). Trí tuệ nhân tạo là một lĩnh vực liên quan đến chuyên ngành khoa học máy tính và công nghệ thông tin, bản chất của trí tuệ nhân tạo vẫn do con người làm ra, họ xây dựng các thuật toán, lập trình bằng các công cụ phần mềm công nghệ thông tin, giúp các máy tính có thể tự động xử lý các hành vi thông minh như con người.

[3] Trí tuệ nhân tạo có khả năng tự thích nghi, tự học và tự phát triển, tự đưa ra các lập luận để giải quyết vấn đề, có thể giao tiếp như người…tất cả là do AI được cài một cơ sở dữ liệu lớn, được lập trình trên cơ sở dữ liệu đó và tái lập trình trên cơ sở dữ liệu mới sinh ra. Cứ như vậy cấu trúc của AI luôn luôn thay đổi và thích nghi trong điều kiện và hoàn cảnh mới. Dự báo đến năm 2030 của công ty kiểm toán và tư vấn tài chính PwC, GDP toàn cầu có thể tăng trưởng thêm 14% từ sự hỗ trợ của trí tuệ nhân tạo, AI đã xuất hiện trong nhiều ngành, từ cung cấp dịch vụ mua sắm ảo và ngân hàng trực tuyến đến giảm chi phí đầu tư trong sản xuất và hợp lý hoá chẩn đoán trong chăm sóc sức khoẻ. AI đã thúc đẩy hầu hết các ngành công nghiệp tiến lên và thay đổi cuộc sống của nhiều người.

[4] Trong lịch sử phát triển của mình từ năm 1960 đến năm 2018, thế giới đã có gần 340.000 sáng chế đồng dạng và hơn 1,6 triệu bài báo khoa học liên quan đến phát triển trí tuệ nhân tạo được công bố. Trong thập niên 80, AI đã bắt đầu được quan tâm, nhưng đến những năm 2012 sự tăng tốc mới trở nên mạnh mẽ. Giai đoạn 2006-2012, số công bố sáng chế bình quân tăng 8% trong một năm, nhưng đến giai đoạn 2012-2017 mức tăng đã đạt 28% trong một năm. Số lượng đơn sáng chế liên quan đến AI tăng từ 8.515 trong năm 2006 lên đến 12.473 năm 2011 và 55.660 năm 2017 (tăng gấp 6, 5 lần trong vòng 12 năm).

[5] Trong nghiên cứu khoa học, các công bố bài báo liên quan đến AI cũng tăng lên rất nhanh chóng, đặc biệt trong thời gian đến năm 2018 gần đây với 1.636.649 bài báo được công bố. Sự xuất hiện của các bài báo khoa học về AI bắt đầu sớm hơn 10 năm trước khi diễn ra cuộc chạy đua bảo hộ sáng chế công nghệ AI. Chứng tỏ, kết quả của nghiên cứu khoa học cơ bản về AI đã có hiệu quả về mặt ứng dụng khi các cuộc đua đăng ký bảo hộ sáng chế gia tăng sau đó.

[6] Theo hệ thống phân loại của Hiệp hội Máy tính Quốc tế ACM (Computing Analysis Scheme) có một khung phân tích rõ ràng phù hợp để tổng hợp và đại diện cho công nghệ đang thay đổi AI theo thời gian. Phân loại này đã được sử dụng trong hơn 50 năm và bản cập nhật cuối cùng vào năm 2012 đã bổ sung các công nghệ mới. Theo đó, công nghệ AI được chia thành 3 hướng chính:

- Kỹ thuật AI (AI Technique): là các mô hình tính toán và thống kê tiên tiến như học máy, logic mờ và hệ thống cơ sở tri thức cho phép tính toán, nhiệm vụ do con người thực hiện; Các kỹ thuật trí tuệ nhân tạo khác nhau được sử dụng để thực hiện các chức năng khác nhau.

 - Ứng dụng chức năng của trí tuệ nhân tạo (AI functions application): chẳng hạn như thị giác máy tính (computer vision) có thể chứa một hoặc nhiều kỹ thuật trí tuệ khác nhau.

- Ứng dụng trí tuệ nhân tạo theo lĩnh vực (AI Application field ): là việc sử dụng các kỹ thuật hoặc ứng dụng trí tuệ nhân tạo chức năng trong các lĩnh vực, ngành nghề cụ thể như giao thông vận tải, nông nghiệp, khoa học đời sống, y tế ...

XEM TOÀN BỘ ĐỀ