Đề thi thử đánh giá tư duy ĐH Bách khoa Hà Nội số 3 - Tuyensinh247 (có đáp án)
Cập nhật lúc: 16:33 21-06-2023 Mục tin: Đề thi đánh giá tư duy
Đề thi thử và hướng dẫn giải chi tiết đề thi thử đánh giá tư duy ĐH Bách khoa Hà Nội số 3 của Tuyensinh247 được cập nhật và đăng tải bên dưới.
Xem thêm:
CẤU TRÚC BÀI THI
|
Phần thi |
Số câu |
Thời gian ( phút) |
|
Phần 1. Tư duy toán học |
40 |
60 |
|
Phần 2. Tư duy đọc hiểu |
20 |
30 |
|
Phần 3.Tư duy khoa học/Giải quyết vấn đề |
40 |
60 |
|
Tổng |
100 câu |
150 phút |
-----------------------------------------------
NỘI DUNG BÀI THI
BIÊN SOẠN: BAN CHUYÊN MÔN TUYENSINH247.COM
PHẦN 1. TƯ DUY TOÁN HỌC
Câu 1: Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(A\) có \(BC = 2a\), cạnh bên \(SA\) vuông góc với đáy và \(SA = a\sqrt 2 \). Thể tích khối chóp \(S.ABC\) là?
A. \(2\sqrt 2 {a^3}\).
B. \(\dfrac{{\sqrt 2 {a^3}}}{3}\).
C. \(\sqrt 2 {a^3}\).
D. \(\dfrac{{2\sqrt 2 {a^3}}}{3}\)
Câu 2: Có ........... số phức \(z\) thỏa mãn \(\left| z \right|\left( {z - 5 - i} \right) + 2i = \left( {6 - i} \right)z\).
Câu 3: Trò chơi quay bánh xe số trong chương trình truyền hình "Hãy chọn giá đúng" của kênh VTV3 Đài truyền hình Việt Nam, bánh xe số có 20 nấc điểm: 5, 10, 15, …, 100 với vạch chia đều nhau và giả sử rằng khả năng chuyển từ nấc điểm đã có tới các nấc điểm còn lại là như nhau. Trong mỗi lượt chơi có 2 người tham gia, mỗi người được quyền chọn quay 1 hoặc 2 lần, và điểm số của người chơi được tính như sau:
+ Nếu người chơi chọn quay 1 lần thì điểm của người chơi là điểm quay được.
+ Nếu người chơi chọn quay 2 lần và tổng điểm không lớn hơn 100 thì điểm của người chơi là tổng điểm quay được.
+ Nếu người chơi chọn quay 2 lần và tổng điểm lớn hơn 100 thì điểm của người chơi là tổng điểm quay được trừ đi 100.
Luật chơi quy định, trong mỗi lượt chơi người nào có điểm số cao hơn sẽ thắng cuộc, hòa nhau sẽ chơi lại lượt khác. An và Bình cùng tham gia một lượt chơi, An chơi trước và có điểm số là 75. Xác suất để Bình thắng cuộc ngay ở lượt chơi này là?
A. \(\dfrac{7}{{16}}\).
B. \(\dfrac{3}{{16}}\).
C. \(\dfrac{{19}}{{40}}\).
D. \(\dfrac{1}{4}\)
Câu 4: Tìm tất cả các giá trị của \(m\) để phương trình \(\ln \left[ {m + \ln \left( {m + \sin x} \right)} \right] = \sin x\) có nghiệm.
A. \(\dfrac{1}{e} + 1 \le m \le e - 1\).
B. \(1 \le m \le e - 1\).
C. \(1 \le m \le \dfrac{1}{e} + 1\).
D. \(1 \le m \le e - 1\).
Câu 5: Trong không gian \(Oxyz\) cho 4 điểm \(A(0;1; - 1)\), \(B(1;1;2)\), \(C(1; - 1;0)\) và \(D(0;0;1)\). Mặt phẳng \((\alpha )\) song song với mặt phẳng \((BCD)\) và chia khối tứ diện \(ABCD\) thành hai phần, sao cho tỉ số thể tích khối tứ diện nhỏ chứ \(A\) và thể tích khối tứ diện \(ABCD\) bằng \(\dfrac{1}{{27}}\).
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
Đúng |
Sai |
|
|
Đường thẳng \(AB\) vuông góc với mặt phẳng \((BCD)\). |
||
|
Phương trình mặt phẳng \((\alpha )\) là \(y - z - 1 = 0\). |
Câu 6: Gọi tất cả các giá trị của \(m > 0\) để giá trị nhỏ nhất của hàm số \(y = {x^3} - 3x + 1\) trên đoạn \([m + 1;m + 2]\) luôn bé hơn 3 là \((a;b)\). Khi đó \(a + b = ........\)
Câu 7: Cho hàm số \(y = f(x)\) xác định trên đoạn \(\left[ {0;\dfrac{\pi }{2}} \right]\) thỏa mãn
\(\int\limits_0^{\dfrac{\pi }{2}} {\left[ {{f^2}(x) - 2\sqrt 2 .f(x).\sin \left( {x - \dfrac{\pi }{4}} \right)} \right]dx} = \dfrac{{2 - \pi }}{2}\)
Giá trị của tích phân \(\int\limits_0^{\dfrac{\pi }{2}} {f(x)dx} \) bằng?
A. \(\dfrac{\pi }{4}\).
B. \(1\).
C. \(0\).
D. \(\dfrac{\pi }{2}\)
Câu 8: Xếp 6 người A, B, C, D, E, F vào ghế dài có 6 chỗ.
Kéo các ô sau thả vào vị trí thích hợp để được khẳng định đúng:
1) Có [vị trí 1] cách xếp sao cho A và F ngồi ở hai đầu ghế.
2) Có [vị trí 2] cách xếp sao cho A và F ngồi cạnh nhau.
3) Có [vị trí 3] cách xếp sao cho A và F không ngồi cạnh nhau.

Câu 9: Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là \(18\pi \,{{d}}{{{m}}^{{3}}}\). Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Thể tích \(V\) của nước còn lại trong bình bằng?

A. \(24\pi \,(d{m^3})\).
B. \(12\pi \,(d{m^3})\).
C. \(54\pi \,(d{m^3})\).
D. \(6\pi \,(d{m^3})\)
Câu 10: Số nghiệm của phương trình \(\sin 5x + \sqrt 3 \cos 5x = 2\sin 7x\) trên khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\) là .............
Câu 11: Cho dãy số \(\left( {{u_n}} \right)\) được xác định như sau \({u_1} = 2016;{u_{n - 1}} = {n^2}\left( {{u_{n - 1}} - {u_n}} \right)\), với mọi \(n \in {\mathbb{N}^*},n \ge 2\). Giới hạn của dãy số \(\left( {{u_n}} \right)\) bằng?
A. \(1011\).
B. \(1010\).
C. \(1008\).
D. \(1009\)
Câu 12: Cho số phức z thỏa mãn \(\left| {z + \overline z } \right| + \left| {z - \overline z } \right| = 4\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(P = \left| {z - 2 - 2i} \right|\). Đặt \(A = M + m\). Những mệnh đề nào sau đây là đúng?
A. \(4 < A < 5\).
B. \(5 < A < 6\).
C. \(A > 5,6\).
D. \(A < 5,4\)
Câu 13: Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(4a\), cạnh bên bằng \(2\sqrt 3 a\) và \(O\) là tâm của đáy. Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là hình chiếu vuông góc của \(O\) lên các mặt phẳng \((SAB)\), \((SBC)\), \((SCD)\)và \((SDA)\). Thể tích của khối chóp \(O.MNPQ\) bằng
A. \(\dfrac{4}{3}{a^3}\).
B. \(\dfrac{{64{a^3}}}{{81}}\).
C. \(\dfrac{{128}}{{81}}{a^3}\).
D. \(\dfrac{{2{a^3}}}{3}\)
Câu 14: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
Đúng |
Sai |
|
|
Chữ số tận cùng của \({9^{{9^{10}}}}\) là 9. |
||
|
Số dư của \({3^{1000}}\) khi chia cho 5 là 2. |
Câu 15: Cho dãy số \(({u_n})\) được xác định bởi \(\left\{ \begin{array}{l}{u_1} = 2019\\{u_n} = - \dfrac{{2019}}{n}({u_1} + {u_2} + {u_3} + ... + {u_{n - 1}}),\,n > 1\end{array} \right.\).
Giá trị của biểu thức \(A = 2{u_1} + {2^2}{u_2} + ... + {2^{2019}}{u_{2019}}\) bằng ...........
Câu 16: Cho hàm số \(f\left( x \right)\) thỏa mãn \(f'\left( x \right) = \left( {x + 1} \right)\left( {3 - x} \right)\sqrt {x - 2} \). Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đồng biến trên (2;3)
B. Hàm số đồng biến trên \(\left( {2; + \infty } \right)\)
C. Hàm số đồng biến trên \(\left( {3; + \infty } \right)\)
D. Hàm số nghịch biến trên \(\left( {2; + \infty } \right)\)
Câu 17: Trong các hàm số sau, những hàm số nào vừa có khoảng đồng biến, vừa có khoảng nghịch biến trên tập xác định của nó?
\(\left( I \right)y = \dfrac{{2x + 1}}{{x + 1}}\), \(\left( {II} \right)y = - {x^4} + 2{x^2} - 2\), \(\left( {III} \right)y = {x^3} + 3x - 4\), \(\left( {IV} \right)y = {x^2} + 1\)
A. Hàm (I)
B. Hàm (II)
C. Hàm (III)
D. Hàm (IV)
Câu 18: Hàm số \(y = f(x)\) có đạo hàm thỏa mãn \({f^\prime }(x) \ge 0,\forall x \in (1;4);{f^\prime }(x) = 0 \Leftrightarrow x \in \left[ {2;3} \right]\). Các khẳng định sau là đúng hay sai?
|
Sai |
Đúng |
|
|
Hàm số \(f(x)\) đồng biến trên khoảng \((1;2)\). |
||
|
\(f(\sqrt 5 ) = f(\sqrt 7 )\) |
||
|
Hàm số \(f(x)\) đồng biến trên khoảng \((1;4)\). |
Câu 19: Có bao nhiêu giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(y = \dfrac{{x - {m^2} - 2}}{{x - m}}\) trên đoạn [0;4] bằng -1.
A. 3 .
B. 2 .
C. 1 .
D. 0 .
Câu 20: Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bời công thức \(c(t) = \dfrac{t}{{{t^2} + 1}}(mg/L)\). Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ
B. 1 giờ
C. 3 giồ
D. 2 giờ
Câu 21: Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oxy , trong đó t là thời gian kể từ khi quả bóng được đá lên; h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó đạt độ cao 6m. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên?
A. \(1\left( s \right)\)
B. \(2,25\left( s \right)\)
C. \(2,58\left( s \right)\)
D. \(4\left( s \right)\)
Câu 22: Gọi x, y là các số thực dương thỏa mãn điều kiện \({\log _9}x = {\log _6}y = {\log _4}(x + y)\) và \(\dfrac{x}{y} = \dfrac{{ - a + \sqrt b }}{2}\) với a, b là các số nguyên dương. Tính \(a + b\).
A. 11
B. 4
C. 6
D. 8
Câu 23: Cho dãy số \(\left( {{u_n}} \right)\), với \({u_n} = \dfrac{1}{{1.4}} + \dfrac{1}{{2.5}} + \ldots + \dfrac{1}{{n(n + 3)}},\forall n = 1;2;3 \cdots \). Mệnh đề nào sau đây đúng?
A. Dãy số \(\left( {{u_n}} \right)\) bị chặn trên và không bị chặn dưới.
B. Dãy số \(\left( {{u_n}} \right)\) bị chặn dưới và không bị chặn trên.
C. Dãy số \(\left( {{u_n}} \right)\) bị chặn.
D. Dãy số \(\left( {{u_n}} \right)\) không bị chặn.
Câu 24: Khi một vận động viên nhảy dù nhảy ra khỏi máy bay, giả sử quãng đường người ấy rơi tự do (tính theo feet) trong mỗi giây liên tiếp theo thứ tự trước khi bung dù lần lượt là: 16; 48;80;112;144;…(các quãng đường này tạo thành cấp số cộng).
|
Đúng |
Sai |
|
|
Công sai của cấp số cộng trên là d=30 |
||
|
Tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên là 1060 feet |
Câu 25: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Hai mặt phẳng cùng đi qua 3 điểm A, B, C không thẳng hàng thì hai mặt phẳng đó trùng nhau.
Câu 26: Hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và: \(f'\left( x \right) = 2{{{e}}^{2x}} + 1,\)\(\forall x,{\mkern 1mu} f\left( 0 \right) = 2\). Hàm \(f\left( x \right)\) là
A. \(y = 2{{{e}}^x} + 2x\).
B. \(y = 2{{{e}}^x} + 2\).
C. \(y = {{{e}}^{2x}} + x + 2\).
D. \(y = {{{e}}^{2x}} + x + 1\).
Câu 27: Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + x + 1\;\;khi\;x \ge 0}\\{2x + 1\;\;\;\;\;\;\;khi\;x \le 0}\end{array}} \right.\). Biết \(\int\limits_0^{\dfrac{\pi }{2}} {f\left( {2\sin x - 1} \right)} .\cos xdx + \int\limits_e^{{e^2}} {\dfrac{{f\left( {\ln x} \right)}}{x}} {{ \;}} = \dfrac{a}{b}\) với \(\dfrac{a}{b}\) là phân số tối giản. Giá trị của \(a.b\) bằng
A. 60
B. 92
C. 174
D. 132
Câu 28: Một chất điểm chuyển động trên đường thẳng nằm ngang với gia tốc phụ thuộc thời gian \(t(s)\) là \(a(t) = 4t - 1\)\((m/{s^2})\). Biết vận tốc ban đầu bằng \(15(m/s)\), hỏi sau bao lâu thì chất điểm đạt vận tốc tốc \(25(m/s)\)?
A. \(t = 3{{s}}\)
B. \(t = 2{{s}}\)
C. \(t = 2,5{{s}}\)
D. \(t = 4{{s}}\)
Câu 29: Tìm hai số thực \(x\) và \(y\) thỏa mãn \(\left( {2x - 3yi} \right) + \left( {3 - i} \right) = 5x - 4i\) với \(i\) là đơn vị ảo.
A. \(x = {{ \;}} - 1;y = {{ \;}} - 1\).
B. \(x = {{ \;}} - 1;y = 1\).
C. \(x = 1;y = {{ \;}} - 1\).
D. \(x = 1;y = 1\).
Câu 30: Trong tổ Toán có 25 giáo viên. Ngày họp đầu năm, mỗi giáo viên trong tổ chào nhau bằng một cái bắt tay một lần với tất cả giáo viên trong tổ. Hỏi có tất cả có bao nhiêu cái bắt tay.
A. 300
B. 24
C. 25
D. 25!
Câu 31: Một bình đựng 25 quả cầu phân biệt, trong đó có 10 quả cầu màu xanh và 15 quả cầu màu đỏ. Chọn ngẫu nhiên 5 quả cầu xác suất để trong 5 quả cầu được chọn có cả quả cầu màu xanh và quả cầu màu đỏ là
A. \(\dfrac{{475}}{{507}}\)
B. \(\dfrac{{475}}{{506}}\)
C. \(\dfrac{{457}}{{506}}\)
D. \(\dfrac{{477}}{{506}}\)
Câu 32: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại A, AB = a. Biết A'B tạo với đáy một góc bằng 60 độ. Thể tích khối lăng trụ bằng:
A. \(\dfrac{3}{2}{a^3}\).
B. \(\dfrac{{\sqrt 3 }}{2}{a^3}\).
C. \(\dfrac{{\sqrt 3 }}{4}{a^3}\).
D. \(\dfrac{1}{2}{a^3}\).
Câu 33: Tính thể tích \(V\) của khối nón có chiều cao \(h = 3a\) và bán kính đáy \(r = a\sqrt 5 \).
A. \(V = \dfrac{{\pi {a^3}\sqrt 5 }}{3}\)
B. \(V = 5\pi {a^3}\)
C. \(V = \dfrac{{\pi {a^3}}}{3}\)
D. \(V = 3\pi {a^3}\)
Câu 34: Cho hình chóp S.ABCD có đáy là hình chữ nhật với \(AB = 3a\), \(BC = 4a\), \(SA = 12a\) và SA vuông góc với đáy. Tính bán kính \(R\) của mặt cầu ngoại tiếp hình chóp S.ABCD.
A. \(R = \dfrac{{13a}}{2}\)
B. \(R = 6a\)
C. \(R = \dfrac{{5a}}{2}\)
D. \(R = \dfrac{{17a}}{2}\)
Câu 35: Trong không gian Oxyz, cho điểm \(A\left( {2; - 1;0} \right)\) và mặt phẳng \(\left( P \right)\): \(3x + y + z + 10 = 0\). Phương trình mặt phẳng \(\left( Q \right)\) đi qua điểm \(A\) và song song với mặt phẳng \(\left( P \right)\) là:
A. \(\left( Q \right):3x + y + z + 5 = 0\).
B. \(\left( Q \right):3x - y + z - 5 = 0\).
C. \(\left( Q \right):3x + y + z - 5 = 0\).
D. \(\left( Q \right):3x - y + z + 5 = 0\).
Câu 36: Lập phương trình mặt cầu (S) qua 2 điểm \(A(2;6;0),B(4;0;8)\) và có tâm thuộc \(d\) : \(\dfrac{{x - 1}}{{ - 1}} = \dfrac{y}{2} = \dfrac{{z + 5}}{1}\).
A. \(({{S}}):{\left( {x + \dfrac{{32}}{3}} \right)^2} + {\left( {y - \dfrac{{58}}{3}} \right)^2} + {\left( {z - \dfrac{{44}}{3}} \right)^2} = 932\)
B. \(({{S}}):{\left( {x - \dfrac{{32}}{3}} \right)^2} + {\left( {y + \dfrac{{58}}{3}} \right)^2} + {\left( {z + \dfrac{{44}}{3}} \right)^2} = 932\)
C. \(({{S}}):{\left( {x - \dfrac{{32}}{3}} \right)^2} + {\left( {y - \dfrac{{58}}{3}} \right)^2} + {\left( {z + \dfrac{{44}}{3}} \right)^2} = 932\)
D. \(({{S}}):{\left( {x - \dfrac{{32}}{3}} \right)^2} + {\left( {y + \dfrac{{58}}{3}} \right)^2} + {\left( {z - \dfrac{{44}}{3}} \right)^2} = 932\)
Câu 37: Trong không gian Oxyz, cho đường thẳng \(d:\dfrac{{x + 2}}{{m + 2}} = \dfrac{{y - 1}}{{2m - 1}} = \dfrac{{z - 3}}{1}\) và mặt phẳng \(\left( P \right):2x + y + z - 4 = 0\), hai điểm \(A\left( {0;2;2} \right),{\mkern 1mu} {\mkern 1mu} B\left( {1;1;1} \right)\) thuộc \(\left( P \right)\). Giá trị của \(m\) để AB vuông góc với hình chiếu của \(d\) trên \(\left( P \right)\) là
A. \(m = 2\).
B. \(m = {{ \;}} - 2\).
C. \(m = {{ \;}} - \dfrac{2}{3}\).
D. \(m = \dfrac{2}{3}\).
Câu 38: Cho một số có hai chữ số. Nếu đổi chỗ hai chữ số của nó thì được một số lớn hơn số đã cho là 63. Tổng của số đã cho và số mới tạo thành 99. Tổng hai chữ số của số đã cho là
A. 9
B. 18
C. 81
D. 36
Câu 39: Cho \(A = \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + ... + \dfrac{1}{{n\left( {n + 1} \right)}}\). Tìm \(\left[ A \right]\)
A. 0
B. 1
C. 2
D. 3
Câu 40: Cho hàm số \(y = f(x)\) liên tục trên đoạn \([ - 1;6]\) và có đồ thị là đường gấp khúc A B C trong hình bên. Biết \(F\) là nguyên hàm của \(f\) thỏa mãn \(F( - 1) = - 1\). Giá trị của \(F(5) + F(6)\) bằng?
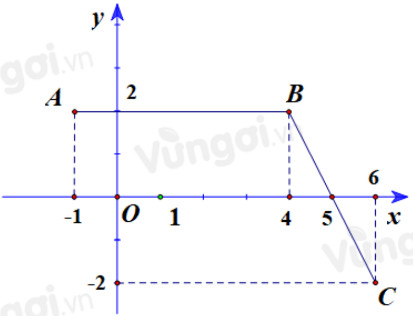
A. 21 . B. 25 . C. 23 . D. 19 .
PHẦN 2. TƯ DUY ĐỌC HIỂU
Đọc văn bản sau và trả lời các câu hỏi từ 1 đến 10:
Tìm hiểu về hiện tượng El Nino và La Nina
[1] Hiện nay, vấn đề làm cho không chỉ Việt Nam mà cả thế giới phải quan tâm đó là sự nóng lên toàn cầu. Hiện tượng này làm cho thời tiết thay đổi thất thường với những diễn biến phức tạp và khó lường như băng tan nhanh và mực nước biển dâng cao. Với sự biến đổi khí hậu toàn cầu ngày càng nghiêm trọng thì các nhà khoa học đã tiến hành nghiên cứu để tìm ra nguyên nhân và họ chú ý đặc biệt đến El Nino và La Nina. Vậy El Nino và La Nina là gì? và nó tác động thế nào đến trái đất chúng ta hiện nay?
[2] “El Nino” (theo tiếng Tây Ban Nha có nghĩa là đứa con của Chúa hay còn gọi là bé Hài Đồng nam) là từ được dùng để chỉ hiện tượng nóng lên dị thường của lớp nước biển bề mặt ở khu vực xích đạo trung tâm và Đông Thái Bình Dương, kéo dài 8 - 12 tháng, hoặc lâu hơn, thường xuất hiện 3 - 4 năm 1 lần, song cũng có khi dày hơn hoặc thưa hơn.

[3] Lịch sử nghiên cứu: Vào năm 1920, một nhà khoa học Anh tên là Gibert Walker, khi nghiên cứu biến động của gió mùa, trong quá trình làm việc ông đã tìm được một số loại hình mưa của Nam Mỹ với sự thay đổi của nhiệt độ đại dương. Ông cũng là người phát hiện đầu tiên mối quan hệ khí áp ở phía Đông và Tây Thái Bình Dương, ông gọi đây là dao động Nam bán cầu (Southern Oscillation). Ngoài ra, ông còn nhận thấy khí áp phía Đông Thái Bình Dương giảm thường liên quan đến hạn hán ở Australia, Ấn Độ và một phần Châu Phi, làm cho mùa Đông ở Canada ấm lên. Tuy nhiên, để chứng minh cho các kết luận này cần có số liệu nhiệt độ ở vùng biển đó và số liệu trường gió trên cao, nhưng do điều kiện kỹ thuật lúc bấy giờ chưa đáp ứng được nên phải mấy chục năm sau phát hiện của ông mới được công nhận. Đến năm 1966, một nhà khí tượng người Nauy là Jacob Bjerknes đã phát hiện ra tương tác hai chiều giữa đại dương và khí quyển. Ông giải thích sự ấm lên của nước biển trong suốt dải xích đạo từ ngoài khơi Nam Mỹ đến giữa Thái Bình Dương có liên quan đến sự yếu đi của đới gió tín phong.
[4] Như vậy, khái niệm El Nino là kết quả tương tác giữa khí quyển và đại dương mà thể hiện chủ yếu là hoàn lưu khí quyển với nhiệt độ nước biển bề mặt ở khu vực xích đạo Thái Bình Dương, sự thay đổi của một phía sẽ gây ra phản ứng của phía kia. El Nino không phải là một hiện tượng mang tính cục bộ ở vùng biển ngoài khơi Nam Mỹ, mà là một phần hệ thống tương tác có quy mô lớn, phức tạp giữa khí quyển và đại dương. El Nino là một phần của bộ máy khí hậu ở vùng nhiệt đới có liên quan đến nhiều hiện tượng thời tiết thế giới, sự xuất hiện của hiện tượng El Nino biểu hiện sự dao động trong cơ chế của khí hậu toàn cầu.
“La Nina” (hay còn gọi là bé Hài Đồng nữ) là hiện tượng lớp nước biển bề mặt ở khu vực nói trên lạnh đi dị thường, xảy ra với chu kỳ tương tự hoặc thưa hơn El Nino.
Để thể hiện sự ngược nhau giữa hai hiện tượng này có khi người ta dùng khái niệm Anti-El Nino (đối El Nino). Hiện tượng La Nina có thể xuất hiện ngay khi hiện tượng El Nino suy yếu, nhưng có khi không phải như vậy.
[5] ENSO là chữ viết tắt của các từ ghép El Nino Southern Oscillation (El Nino - Dao động Nam) để chỉ cả 2 hai hiện tượng El Nino và La Nina và có liên quan với dao động của khí áp giữa 2 bờ phía Đông Thái Bình Dương với phía Tây Thái Bình Dương - Đông Ấn Độ Dương (Được gọi là Dao động Nam) để phân biệt với dao động khí áp ở Bắc Đại Tây Dương).
DÀNH CHO 2K8 – ÔN THI ĐÁNH GIÁ NĂNG LỰC 2026!
Bài thi Đánh giá năng lực 2026 thay đổi toàn bộ từ cấu trúc bài thi, các dạng câu hỏi,.... mà bạn chưa biết phải ôn tập như thế nào cho hiệu quả? không học môn đó thì làm bài ra sao?
Bạn cần phương pháp ôn tập và làm bài thi từ những người am hiểu về kì thi và đề thi?
Bạn cần thầy cô đồng hành suốt quá trình ôn luyện?
Vậy thì hãy xem ngay lộ trình ôn thi bài bản tại ON.TUYENSINH247.COM:
- Học live, luyện đề cùng giáo viên và Thủ khoa ĐGNL
- Trang bị phương pháp làm bài suy luận khoa học
- Bộ 15+ đề thi thử chuẩn cấu trúc mới bài thi ĐGNL
Xem thêm thông tin khoá học & Nhận tư vấn miễn phí - TẠI ĐÂY
Các bài khác cùng chuyên mục
- Đề ôn thi đánh giá tư duy ĐHBKHN năm 2025 - Phần Tư duy đọc hiểu (số 2)(07/05)
- Đề ôn thi ĐGTD Đại học Bách khoa Hà Nội - Tư duy đọc hiểu 2025(29/04)
- Cấu trúc đề thi đánh giá tư duy 2025 Đại học Bách khoa Hà Nội(12/06)
- Đề minh họa thi đánh giá tư duy mới nhất(25/03)
- Đề thi thử đánh giá tư duy Bách khoa có đáp án - Tuyensinh247 (Đề 6)(29/12)
- Đề thi thử đánh giá tư duy ĐHBK Hà Nội - Phần Khoa học/Giải quyết vấn đề (số 4)(16/11)
- Đề 5 - thi thử đánh giá tư duy ĐH Bách khoa Hà Nội có đáp án (Tuyensinh247)(15/11)
- Đề thi thử đánh giá tư duy ĐHBK Hà Nội số 5 - phần Tư duy đọc hiểu(17/10)
- Đề 3 - thi thử đánh giá tư duy ĐHBKHN phần Khoa học/Giải quyết vấn đề(14/10)
- Đề thi thử đánh giá tư duy Phần Khoa học/Giải quyết vấn đề - Đề 2(12/10)
chuyên đề được quan tâm
bài viết mới nhất
- Danh sách các tổ hợp xét đại học và các...
- Lịch thi Đánh giá tư duy - TSA năm 2026...
- Danh sách trường xét điểm thi Đánh giá tư duy...
- Đề ôn thi đánh giá tư duy ĐHBKHN năm 2025...
- Phổ điểm thi Đánh giá tư duy 2025 - 3...
- Phổ điểm thi TSA đợt 3 năm 2025
- Đề ôn thi ĐGTD Đại học Bách khoa Hà Nội...
- Phổ điểm thi Đánh giá tư duy đợt 2 ĐH...
- Video hướng dẫn đăng ký thi TSA - ĐH Bách...
- Phổ điểm thi Đánh giá tư duy - ĐHBKHN đợt...
Trang thông tin mới nhất năm 2026 về kì thi đánh giá tư duy của trường Đại học Bách Khoa Hà Nội giúp trả lời rõ ràng tất cả câu hỏi như: Thi ĐGTD là gì, Đề thi đánh giá tư duy cấu trúc thế nào, gồm bao nhiêu phần, thời gian thi, thời gian mỗi phần, mỗi câu bao nhiêu điểm, lịch thi khi nào, thi ở đâu...


