Đề thi thử đánh giá tư duy ĐHBKHN số 4 có đáp án - Tuyensinh247

CẤU TRÚC BÀI THI

-----------------------------------------

NỘI DUNG BÀI THI

BIÊN SOẠN: BAN CHUYÊN MÔN TUYENSINH247.COM

PHẦN I: TƯ DUY TOÁN HỌC

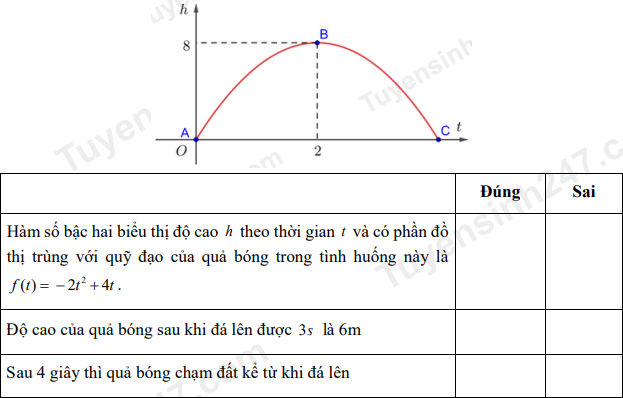
Câu 1. Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Hình minh hoạ quỹ đạo của quả bóng là một phần của cung parabol trong mặt phẳng toạ độ Oth, trong đó \(t\) là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên và \(h\) là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ mặt đất. Sau khoảng \(2\;s\), quả bóng lên đến vị trí cao nhất là \(8\;m\).

Câu 2. Cho hai hàm số \(f(x)\) và \(g(x)\) cùng đồng biến trên khoảng \((a;b)\). Có thể kết luận gì về chiều biến thiên của hàm số \(y = f(x) + g(x)\) trên khoảng \((a;b)\) ?

A. Đồng biến.

B. Nghịch biến.

C. Không đổi.

D. Không kết luận được

Câu 3. Tìm tất cả các giá trị của \(m\) để hàm số \(y = \sqrt { - 2x + 3m + 2}  + \dfrac{{x + 1}}{{x + 2m - 4}}\) xác định trên \(( - \infty ; - 2)\).

A. \(m \in [ - 2;4]\).

B. \(m \in ( - 2;3]\).

C. \(m \in [ - 2;3]\).

D. \(m \in ( - \infty ; - 2]\).

Câu 4. Một doanh nghiệp tư nhân \(A\) chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 (triệu đồng) và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.

A. 30 triệu đồng.

B. 29 triệu đồng.

C. 30,5 triệu đồng.

D. 29,5 triệu đồng.

Câu 5. Cho đồ thị hàm số \(y = a\left| x \right|\)

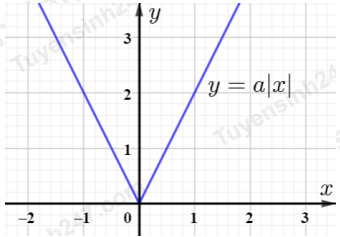
Khi đó giá trị của a là _____

Câu 6. Tìm giá trị thực của tham số \(m \ne 0\) để hàm số \(y = m{x^2} - 2mx - 3m - 2\) có giá trị nhỏ nhất bằng -10 trên \(\mathbb{R}\).

A. \(m = 1\).

B. \(m = 2\).

C. \(m =  - 2\).

D. \(m =  - 1\).

Câu 7. Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số \(y = 2\cos 2x + 5,x \in \left[ {0;\dfrac{\pi }{6}} \right]\) lần lượt là ____ và _____.

Câu 8. Chọn các phát biểu đúng:

(1): Trên \(\mathbb{R}\), hàm số \(y = \cos x\) có tập giá trị là \([ - 1;1]\).

(2): Trên \(\left[ {0;\dfrac{\pi }{2}} \right]\), hàm số \(y = \cos x\) có tập giá trị là [0 ; 1].

(3): Trên \(\left[ {0;\dfrac{{3\pi }}{4}} \right]\), hàm số \(y = \cos x\) có tập giá trị là \(\left[ {0;\dfrac{{\sqrt 2 }}{2}} \right]\).

(4): Trên \(\left[ {0;\dfrac{\pi }{2}} \right)\) hàm số \(y = \cos x\) có tập giá trị là (0 ; 1].

Câu 9. Tìm tập giá trị \(T\) của hàm số \(y = \sqrt {7{{\sin }^2}2x + 9} \).

A. \(T = [3;4]\).

B. \(T = [3;\sqrt {37} ]\).

C. \(T = \mathbb{R}\).

D. \(T = [2;3]\).

Câu 10. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu \(h\) (mét) của mực nước trong kênh được tính tại thời điểm \(t\) (giờ) trong một ngày bởi công thức \(h = 3\cos \left( {\dfrac{{\pi t}}{8} + \dfrac{\pi }{4}} \right) + 12\). Mực nước của con kênh cao nhất khi

A. \(t = 13\) (giờ).

B. \(t = 14\) (giờ).

C. \(t = 15\) (giờ).

D. \(t = 16\) (giờ).

Câu 11. Hàm số nào sau đây là hàm số lẻ trên R ?

A. \(y = {\tan ^2}x\sin x\).

B. \(y = x\cos x\).

C. \(y = {\tan ^3}x\).

D. \(y = 2x\sin 4x\).

Câu 12. Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2,{u_3} = 4\). Tìm số hạng thứ 5 của cấp số nhân đã cho.

A. \({u_5} =  - 8\)

B. \({u_5} = 8\)

C. \({u_5} = 24\)

D. \({u_5} = 6\)

Câu 13. Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 4;{u_2} = 1\). Giá trị của \({u_{10}}\) bằng

A. \({u_{10}} = 31\).

B. \({u_{10}} =  - 23\).

C. \({u_{10}} =  - 20\).

D. \({u_{10}} = 15\).

Câu 14. Gọi S là tập hợp tất cả các giá trị \(x \in (0;10\pi )\) và \(\dfrac{{\sin x}}{2};\sqrt 3 \cos x;\tan x\) theo thứ tự là một cấp số nhân, tính tổng các phần tử của \({\rm{S}}\).

A. \(50\pi \)

B. \(40\pi \)

C. \(36\pi \)

D. \(30\pi \)

Câu 15. Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và \(d =  - 3\). Trên mặt phẳng tọa độ \(Oxy\) lấy các điểm \({A_1},\;{A_2}, \ldots \) sao cho với mỗi số nguyên dương \(n\), điểm \({A_n}\) có tọa độ \(\left( {n;{u_n}} \right)\). Biết rằng khi đó tất cả các điểm \({A_1},{A_2}, \ldots {A_n}, \ldots \) cùng nằm trên một đường thẳng. Viết phương trình đường thẳng đó.

A. \(y + 3x = 5\).

B. \(y + 3x = 2\).

C. \(y = 2x - 3\).

D. \(y = 2x - 5\).

Câu 16. Cho dãy số \(\left( {{u_n}} \right)\) có \({u_n} = {n^2} - 2n + 2\), dãy có bao nhiêu số hạng là số chính phương

A. 0

B. 1

C. 2

D. Vô số.

Câu 17. Cho hàm số \(f(x)\) xác định trên [a ; b]. Tìm mệnh đề đúng.

A. Nếu hàm số \(f(x)\) liên tục trên [a ; b] và \(f(a)f(b) > 0\) thì phương trình \(f(x) = 0\) không có nghiệm trong khoảng \((a;b)\).

B. Nếu \(f(a)f(b) < 0\) thì phương trình \(f(x) = 0\) có ít nhất một nghiệm trong khoảng \((a;b)\).

C. Nếu hàm số \(f(x)\) liên tục, tăng trên [a ; b] và \(f(a)f(b) > 0\) thì phương trình \(f(x) = 0\) không có nghiệm trong khoảng \((a;b)\).

D. Nếu phương trình \(f(x) = 0\) có nghiệm trong khoảng \((a;b)\) thì hàm số \(f(x)\) phải liên tục trên \((a;b)\).

Câu 18. Cho \({u_n} = \dfrac{{5 \cdot {6^{n + 1}} + {2^n}}}{{4 \cdot {6^n} + {3^{n + 2}}}}\). Biết \(\lim {u_n} = \dfrac{a}{b}\) với \(a,b \in {\mathbb{N}^*}\) và \(\dfrac{a}{b}\) là phân số tối giản. Đặt \(S = a + b\), mệnh đề nào dưới đây là đúng?

A. \(10 < S < 20\).

B. \(20 < S < 30\).

C. \(30 < S < 40\).

D. \(40 < S < 50\).

Câu 19. Cho dãy số \(\left( {{u_n}} \right)\) được xác định bời: \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 1}\\{{u_{n + 1}} = {u_n} + \dfrac{1}{{{2^n}}}(n \ge 1)}\end{array}} \right.\). Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

Câu 20. Số thập phân vô hạn tuần hoàn \(0,5111 \ldots \) được biểu diễn bởi phân số tối giản \(\dfrac{a}{b}\). Tính \(a + b\)

A. 17.

B. 68.

C. 133.

D. 137.

Câu 21. Cho \(\mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt {2x + 5}  - 3}}{{x - 2}} = \dfrac{a}{b}\), trong đó a, b là các số nguyên dương và phân số \(\dfrac{a}{b}\) tối giản. Tính giá trị biểu thức \(P = 1984{a^2} + 4{b^2}\).

A. 0.

B. 2000.

C. 8000.

D. 2020 .

Câu 22. Cho a, b là hai số nguyên thỏa mãn \(2a - 5b =  - 8\) và \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt[3]{{ax + 1}} - \sqrt {1 - bx} }}{x} = 4\). Mệnh đề nào dưới đây sai?

A. \(|a| \le 5\).

B. \(a - b > 1\).

C. \({a^2} + {b^2} > 50\).

D. \(a + b > 9\).

Câu 23. Giả sử từ tỉnh A đến tỉnh B có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có 10 chuyến ô tô, 5 chuyến tàu hỏa, 3 chuyến tàu thủy và 2 chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh A đến tỉnh B?

A. 20.

B. 300.

C. 18.

D. 15

Câu 24. Số A = 1078000 có ______ ước số.

Câu 25. Có bao nhiêu số gồm 7 chữ số khác nhau đôi một được lập bằng cách dùng 7 chữ số 1, 2, 3, 4, 5, 7, 9 sao cho hai chữ số chẵn không đứng liền nhau.

Câu 26. Có bao nhiêu số tự nhiên có ba chữ số dạng \(\overline {abc} \) với \(a,b,c \in \{ 1;2;3;4;5;6\} \) sao cho \(a < b < c\).

A. 120 .

B. 30 .

C. 40 .

D. 20 .

Câu 27. Bạn A có 12 bi đỏ, 5 bi xanh và 10 bi vàng. Sau đó bạn A lại cho thêm một số bi đỏ vào. Bạn A lấy ngẫu nhiên 1 viên bi. Xác suất để lấy được bi đỏ là 1/2. Số viên bi đỏ bạn A đã cho thêm là_____

Câu 28. Tìm số hạng không chứa \(x\) trong khai triển \({\left( {{x^2} + \dfrac{2}{x}} \right)^6}\).

A. \({2^4}C_6^2\).

B. \({2^2}C_6^2\).

C. \( - {2^4}C_6^4\).

D. \( - {2^2}C_6^4\).

Câu 29. Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) (tham khảo hình vẽ).

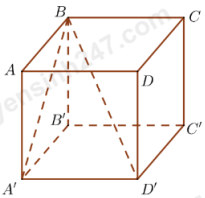
Tính cosin góc giữa hai đường thẳng AD và B D’ là

A. \(\dfrac{{\sqrt 2 }}{{\sqrt 3 }}\).

B. \(\dfrac{{\sqrt 2 }}{3}\).

C. \(\dfrac{{\sqrt 3 }}{4}\).

D. \(\dfrac{{\sqrt 3 }}{3}\).

Câu 30. Cho hai mặt phẳng (P),(Q) vuông góc với nhau. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(1) Góc giữa hai mặt phẳng là \({90^\circ }\).

(2) Mọi đường thẳng trong (P) đều vuông góc với (Q).

(3) Tồn tại đường thẳng trong (Q) vuông góc với (P).

(4) Nếu (R) vuông góc với (Q) thì (R) song song với (P).

(5) Nếu mặt phẳng (R) vuông góc với (P),(R) vuông góc với (Q) thì (R) vuông góc với giao tuyến của (P) và (Q).

A. 3.

B. 4.

C. 1.

D. 5.

Câu 31. Cho hình chóp \(S \cdot ABCD\) có đáy A B C D là hình thoi có cạnh bằng 2 a và \(\widehat {DAB} = {120^\circ }\). Biết hình chiếu vuông góc của đỉnh \(S\) xuống mặt phẳng đáy trùng với trung điểm \(H\) của cạnh A D và tam giác S A D đều. Số đo của góc giữa đường thẳng SH và mặt phẳng \((SBD)\) là _____ (Làm tròn đến hàng đơn vị)

Câu 32. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(A\), \(\widehat {ABC} = {30^\circ }\), tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ điểm \(C\) đến mặt phẳng \((SAB)\) bằng?

A. \(\dfrac{{a\sqrt {39} }}{{26}}\).

B. \(\dfrac{{a\sqrt {39} }}{{13}}\).

C. \(\dfrac{{a\sqrt {13} }}{{13}}\).

D. \(\dfrac{{a\sqrt {13} }}{{26}}\).

Câu 33. Cho hình chóp S . A B C D có mặt bên \((SAB)\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy, \(ABCD\) là hình chữ nhật với \(AB = a,BC = 2a\). Khoảng cách giữa hai đường thẳng \(AC\) và \(SD\) bằng

A. \(\dfrac{{2\sqrt {17} a}}{{17}}\)

B. \(\dfrac{{\sqrt {17} a}}{{17}}\)

C. \(\dfrac{{\sqrt {17} a}}{{34}}\)

D. \(\dfrac{{3\sqrt {17} a}}{{17}}\)

Câu 34. Cho lăng trụ đứng \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy là tam giác cân, AB=AC=a, góc BAC = 120 độ. Mặt phẳng \(\left( {A{B^\prime }{C^\prime }} \right)\) tạo với mặt đáy một góc 60 độ. Tính khoảng cách từ đường thẳng B C đến mặt phẳng \(A{B^\prime }{C^\prime }\) theo \(a\).

A. \(\dfrac{{a\sqrt {35} }}{{21}}\).

B. \(\dfrac{{a\sqrt 7 }}{4}\).

C. \(\dfrac{{a\sqrt 5 }}{{14}}\).

D. \(\dfrac{{a\sqrt 3 }}{4}\).